前言
给定样本$\vec x$,我们用列向量表示该样本$\vec x$=$(x1,x2,x3)^T$。样本有n种特征,我们用x(i)表示样本$\vec x$的第i个特征。
线性模型(linear model)的形式为:
f($\vec x$) = $\vec w$·$\vec x$ + b
代价函数
我们来了解一个机器学习里非常重要的概念,代价函数(cost function)比如我们有一个模型y = $\theta 0$+$\theta 1$x,我们要确定$\theta 0$和$\theta 1$的值
我们简单的定义几个值:
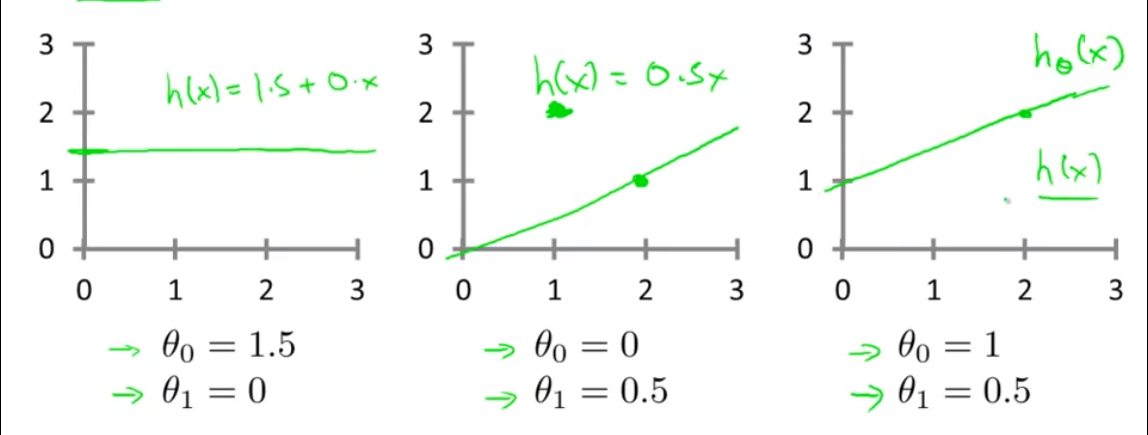
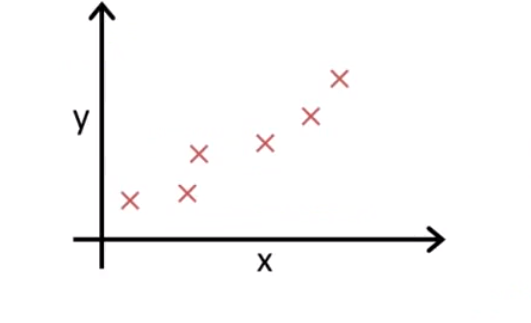
这是一个简单的数据集,我们要使我们的直线尽可能的靠近这些点(拟合):
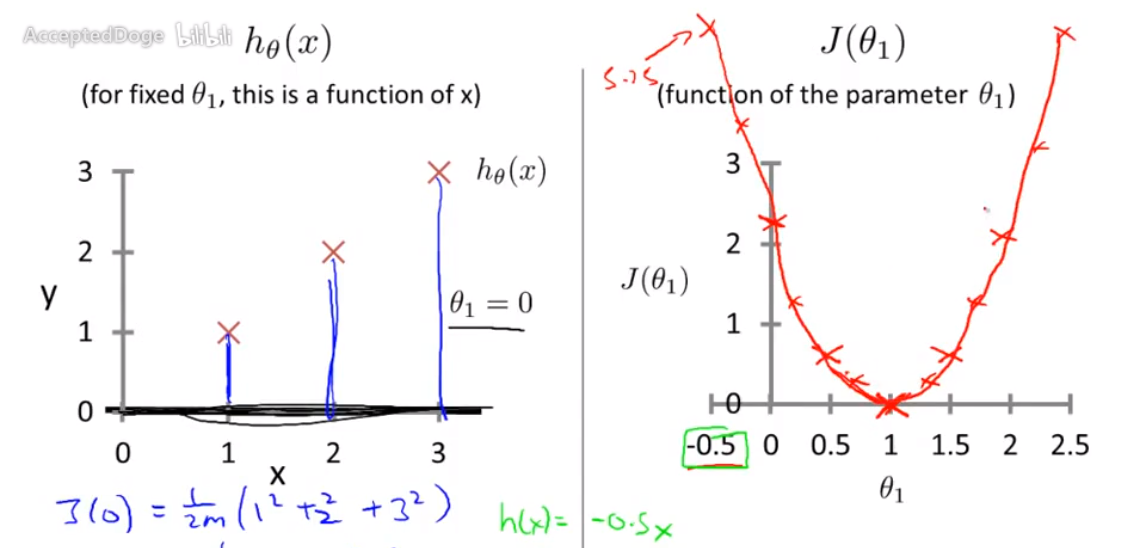
我们如何评定?拿f(x) 和y比较,我们要使这两个的值的差异为最小,这个就是一个误差最小化问题,
我们拿每一个误差相加平方,得公式(求误差均值):$\frac{1}{2m}\sum_{i=1}^m(f(x)^i - y^i)^2$
cost function和模型的对比:
2主要用来化掉该式偏导后得出的常数
上面仅仅是一个特征的代价函数,下面是两个特征的代价函数:
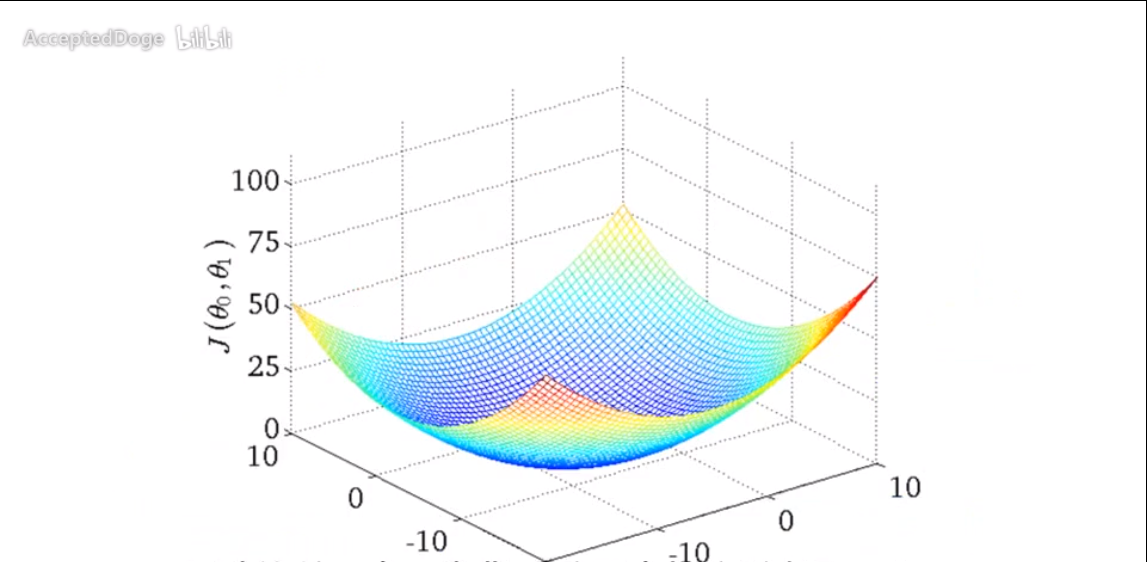
代价函数求最优解
我们如何求到最小值,现在来讲解两种方法,最小二乘法和梯度下降法,
我们回忆一下导数的意义:
导数反映的是函数y=f(x)在某一点处沿x轴正方向的变化率。再强调一遍,是函数f(x)在x轴上某一点处沿着x轴正方向的变化率/变化趋势。直观地看,也就是在x轴上某一点处,如果f’(x)>0,说明f(x)的函数值在x点沿x轴正方向是趋于增加的;如果f’(x)<0,说明f(x)的函数值在x点沿x轴正方向是趋于减少的。
其实就是函数中某点的切线斜率。
偏导数也是一样,不过是对于多元函数,偏导数表示固定面上一点的切线斜率。比如我们发现ƒ在某点与xOz平面平行的切线的斜率是3,记为$\frac{\partial f}{\partial x}$ = 3
最小二乘法:
我们对式内的特征进行偏导,然后对偏导后的式子等于0,就可以求出每个特征权重最优解的闭式解。
这是直接求出最优解的一个方法,我们重点讲一下梯度下降(Gradient Descent):
梯度下降(Gradient Descent):
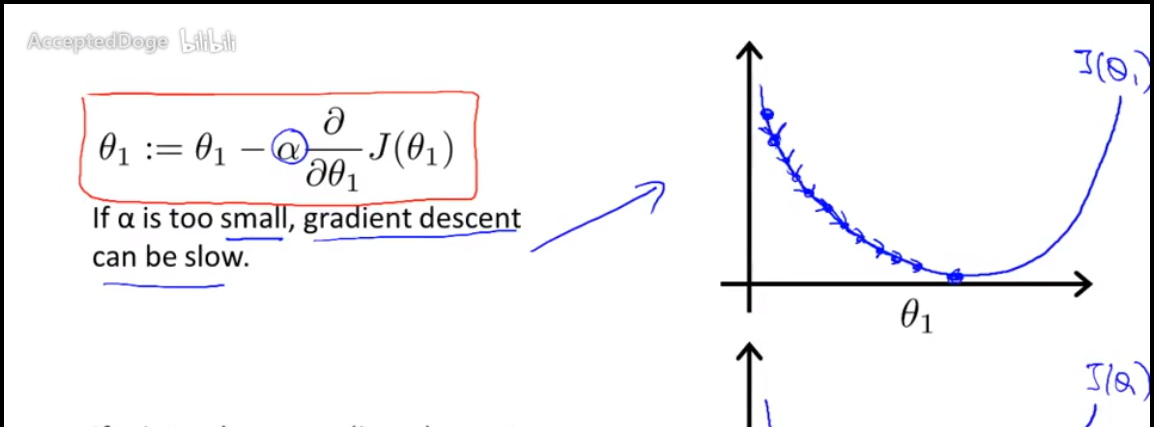
公式:

我们反复执行这个公式,直到收敛,这个公式怎么来的呢??$\alpha$是学习速率,就是我们每一次收敛时候所走的步数。
一个收敛的例子: